> bedはやはりbdを底辺とみると底辺の高さ:高さ= 21で これはeが平行線上にあるからであって、二等辺三角形になるようにeを取った場合に、eが平行線上にあることを示さないといけないだろ?それを聞いてるんだが。直角二等辺三角形の辺の長さの求め方は次のとおり。 直角二等辺三角形・辺の長さの求め方 1 、底辺を求めるときは、斜辺 x を 2 2 x に代入する 2 、斜辺を求めるときは、底辺 x を 2 x に代入する 直角二等辺三角形の辺の長さを求める方法を見ていき 小学校の算数の図形問題には二等辺三角形がたくさん出てくるので、二等辺三角形が出てくるだけで喜ぶ体になったほうが都合がよい。 そこで長方形を見てみよう。 たくさんあってうれしいよ~ 長方形の対角線は4つも二等辺三角形を作ってくれる。
直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
三角形 辺の長さ 求め方 底辺 高さ
三角形 辺の長さ 求め方 底辺 高さ-作図のゴールとなる二等辺三角形の3辺の長さを図に示してあります。 ①底辺をかく ②等しい長さの辺の長さにコンパスを開く ③底辺の両はしにコンパスをさして、ばってんをつくる ④頂点を結ぶ(底辺のはしと、コンパスでできたばってん) 『例題 この記事では、「直角二等辺三角形」の定義や定理(辺の長さの比)について解説していきます。 また、面積の求め方や証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね! 目次 非表示 直角二等辺三角形とは? 定義「3 角のうち




頂角が45 の二等辺三角形の面積 中学数学 Youtube
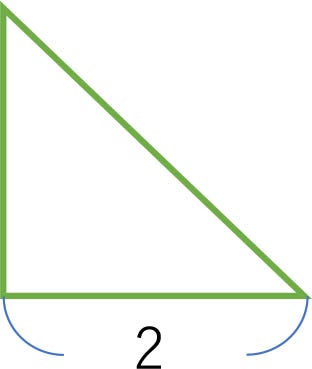
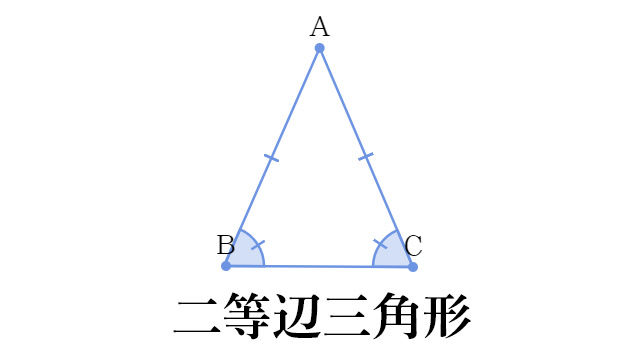
二等辺三角形は次の つの手順で書くことができます。 STEP1 定規で底辺を書く 底辺 は なので、定規で の線分を引きます。 STEP2 底辺の両端にコンパスの針をおき、弧を書く コンパスの幅を線分 と の長さ にとります。 底辺の両端、つまり と にコンパスの針をおき、弧を つずつ書きます。 STEP3 弧の交点と底辺の両端を直線で結ぶ 先ほど書いた つの弧の交点が頂点 です。 点 と点 An Isosceles Triangle(二等辺三角形) 二等辺三角形は、an isosceles triangleと言います。 An isosceles triangle has at least two equal sides (筆者訳)二等辺三角形は、少なくとも長さが同じ2つ辺を有する。 出典:*2 図の三角形は、2つの辺の長さが同じであるため、an isosceles定義をもとに証明されることの中で重要なモノ のことをいいます。 二等辺三角形の定理とは 2つの底角が等しい。 頂角の二等分線は、底辺を垂直に二等分する。 この2つが挙げられるのですが、 これらは「2つの辺が等しい」という定義を用いて次の
二等辺三角形は2つの辺の長さが等しいことで、上のような性質が出てきます。これらの性質がそれぞれ正しいことを確認してみましょう。今回はその2つ目の性質の 頂角の二等分線は、底辺を垂直に二等分する こと確認していきたいと思います。 参考:二等辺三角形の1つ目の性質「2つの角は 締切済 斜辺10cm 頂点の角度30度の二等辺三角形の底辺のながさはいくらになるでしょうか (もとめかたの式と答えがしりたいです) この質問への回答は締め切られました。直角三角形の底辺と斜辺から、高さ・角度・面積を計算します。 底辺と斜辺を入力し「高さ・角度・面積を計算」ボタンをクリックすると、入力された直角三角形の高さと角度と面積が表示されます。 底辺a: 斜辺c:
直角二等辺三角形の辺の比は になります。 この辺の比を覚えておくことで、底辺から斜辺の長さを求めたり、またその逆のことができます。 この章の最後の例題で確認してみてください。 もちろん、 三平方の定理 でもこの比は出せますが、覚えておく このように、二等辺三角形の面積公式を作ることも出来ますが、二等辺三角形だと この公式。直角二等辺三角形だと この公式。と別々に覚えるのは大変ですね。 ですので、やみくもに公式を覚えるのではなく、 が当てはまる、 底辺 と 高さ を探す ほうが 二等辺三角形の定理(性質) 2つの辺が等しいと、いくつかの定理(性質とも言います)ができます。 二等辺三角形の底角は等しい 二等辺三角形の頂角の二等分線は底辺を垂直に二等分する トムソン 暗号かな! ? と思ったかもしれませんが、1つずつ




正方形の1辺を底辺とする二等辺三角形の斜辺の長さを求めよ 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog



面積 直角二等辺三角形 小学4年生算数 そらいろ日記 言葉の宝箱
ユークリッド原論をどう読むか(1) 頁末 前 次 目次 ユークリッド原論 第1巻 命題1ー5(2等辺三角形の底角) 二等辺三角形の 底辺の上にある角は 互いに等しく、 等しい辺が延長される とき、 底辺の下の角は 互いに等しい であろう。二等辺三角形の頂角の定理について・・・、中学二等辺三角形の頂角の定理のまとめをわかりやすく解説します。普段の予習復習から、定期テスト対策、受験対策に活用してください。 ∠bacの二等分線と底辺bcとの交点をdとする。 このときbd=cd、ad⊥bcを 30度二等辺三角形の隠しコマンド 斜辺×斜辺÷4 「底辺 × 高さ ÷ 2」の公式に数字をあてはめるわけですが、この方法で高さを探すと30°二等辺三角形では次のようなことに気づきます。 計算上の底辺=見た目の斜辺 計算上の高さ=見た目の斜辺の半分 ということは、「底辺 × 高さ ÷2」は次のように書き換えることができます。 〔斜辺〕×〔斜辺÷2〕÷〔2〕 カッコをとりはらうと・・



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




世界に1ペアだけ 周りの長さも面積も同じ直角三角形 二等辺三角形 慶大院生ペア証明 朝日新聞デジタル
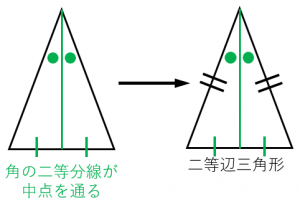
7M デルタループアンテナ 1λ デルタ状態のエレメント全長約4268m になります。エレメントの色は写真の通り青色です。踏みたてを使い垂直9mHi アルミポールの上部に滑車(9M高)にバラン(14)で吊り上げ給電、二等辺三角形状態で設置します。/\の長さ1167m×2 底辺の長11円 ボーネルンド マグ フォーマー 二等辺三角形 12ピース (mfj) ゲーム、おもちゃ パズル ジグソーパズル ゲーム、おもちゃ パズル二等辺三角形を2分割して高さを求める! 二等辺三角形の高さを求めるためには 頂角から垂直に線を引いて 二等辺三角形を2分割してやります。 すると、二等辺三角形の特徴から 底辺の長さが二等分されるんですね。 今回の問題で考えると こういう



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ



二 等辺 三角形 辺 の 長 さ 直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 Stg Origin Aegpresents Com
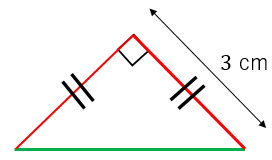
直角二等辺三角形の辺の長さの求め方の2つの公式 求め方には2パターンある。 斜辺以外の辺がわかっているとき 斜辺の長さだけわかっているとき 順番にみていこう! 公式1 「斜辺以外の辺の長さがわかってるとき」 まず、 斜辺以外の長さがわかってるときの場合だね。 つぎの公式で計算できちゃうんだ。 辺の長さをa、斜辺をbとすると、 斜辺b = √2 a になる。 たとえば、 斜辺以外 二等辺三角形は正三角形ではないというのは明らかですよね。 1 正三角形を二等辺三角形といったときは除きます。 では正三角形は二等辺三角形とみることはできるのでしょうか? 正三角形は3辺の長さが等しい三角形なので当然2つの辺の長さは等しいコルムの三角形の場合は,限界変形率が1なので,図1では,公共財と 私的財の間の変換曲線が-1の傾きを持つ直線Fw で描かれている。O AF がA の消費可能な最大公共財水準であり,O Aw がA の消費可能な最大私的財水準で ある。したがって,直角二等辺三角形




二等辺三角形と正三角形 算数用語集




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
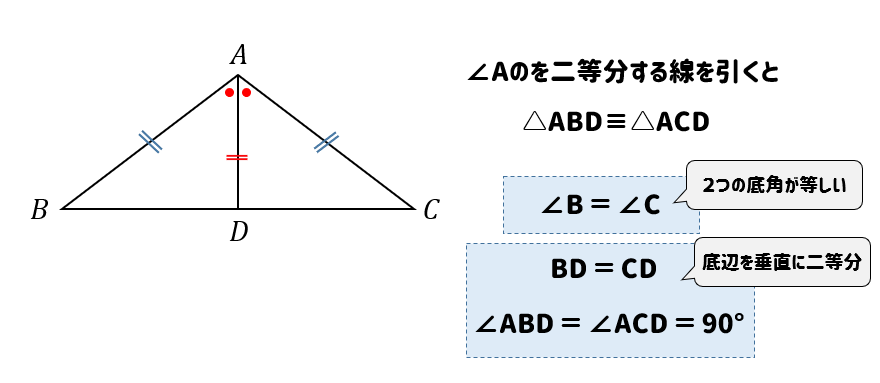
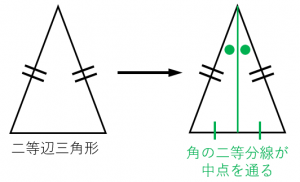
まとめ:二等辺三角形の底辺は二等分線からはじまる。 二等辺三角形の底辺の計算は簡単。 頂角の二等分線を底辺にひく 底辺の半分の長さを求める そいつを2倍する っていう3ステップでいいんだ。 どんどん問題をといてみよう! そんじゃねー Kenここで 頂角を二等分する直線を引き 、底辺との交点を点Dとします。 そして、二等分線を引いてできた ABDと ACDに注目します。 ここで、 ABCは二等辺三角形なので、 AB=AC となります。 以上のことから、 ABDと ACDは2辺とその間の角が等しい合同な三角形になっていることが分かります。二等辺三角形の頂角の二等分線は底辺を 垂直 に二等分する。 三角形の 3 つの内角のうち(少なくとも)2 つの角が等しいものは、二等辺三角形となる(二等辺三角形の成立条件)。 また、対称軸を持つ三角形は二等辺三角形に限られる。 二等辺三角形のうち、3 本の辺の長さが全て等しい三角形は 正三角形 という。 正三角形は、二等辺三角形の特殊な場合である。 正三角形の内角はすべて等しく、



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
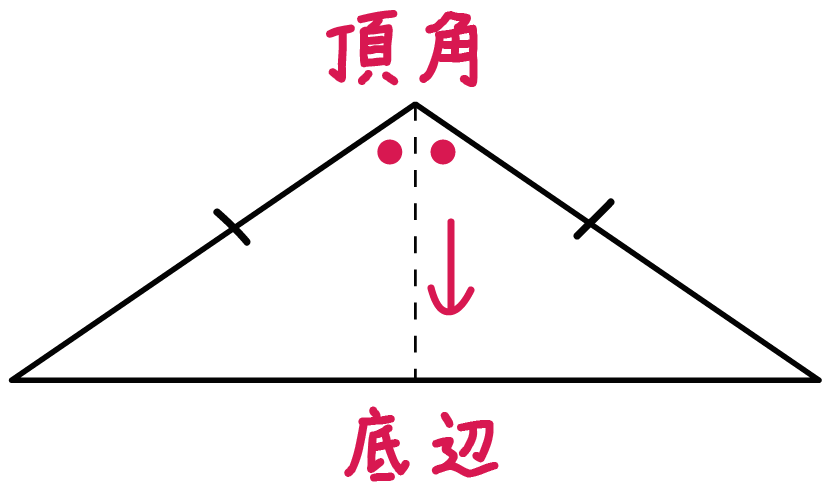
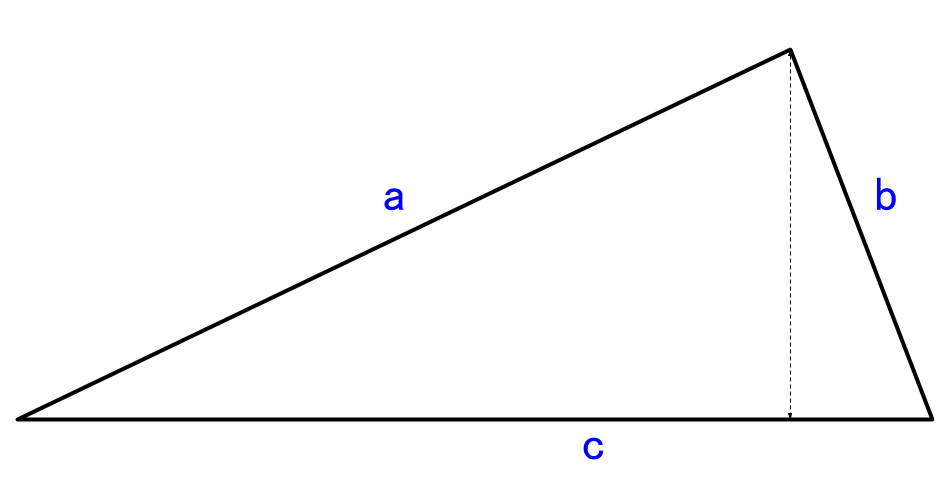
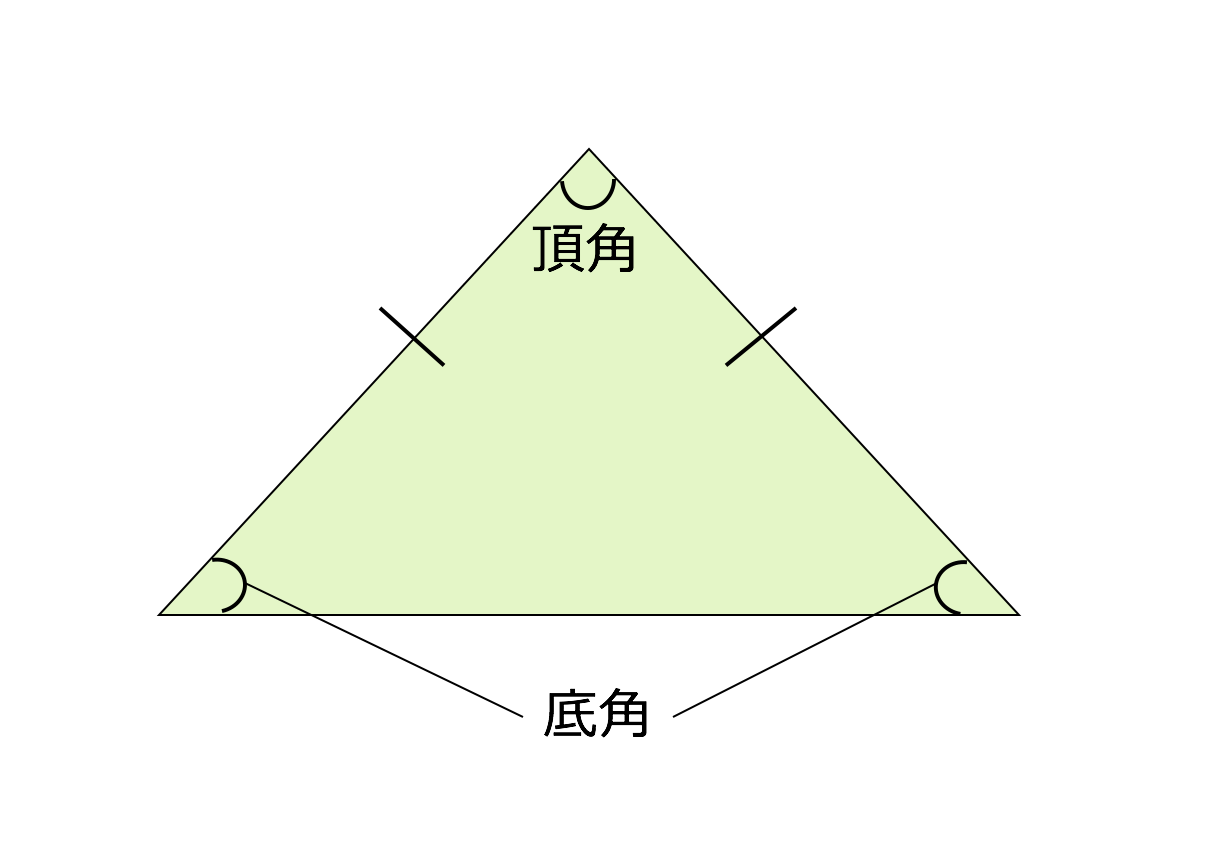
底辺の両端の角∠bと∠cを底角(ていかく) という 二等辺三角形の底角 二等辺三角形の底角は等しい abd≡ acdより bd=cd ∠adb=∠adc つまり,ad⊥bd 二等辺三角形の頂角の二等分線 二等辺三角形の頂角の二等分線は,底辺を垂直に2等分する。二等辺三角形と直角二等辺三角形の公式(面積・高さ・角度・斜辺と周囲の長さ)を解説。 底辺の長さ(b) 100 2 高さ(h) =B1/2 3 斜辺の長さ(a) =B1/SQRT(2) 4 周囲の長さ(L) =(1SQRT(2))*B1 5 面積(S) =B1^2/4 Last update 1424二等辺三角形の底辺BC 底辺 (ていへん)は、 多角形 などの「底部」にある 辺 である。 ただし、 図形 に絶対的な 上下 はないので、紙面や画面上での向きとは無関係に、 計算 などに便利なように底辺を選ぶことができる。 通常は、そうして選んだ底辺が下になるように作画する。 また、底辺を使って 定義 される量に、 高さ がある。 平面図形 の高さは、図形に属する点と底辺との 距離 の 最大値




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の面積を求める算数の公式は
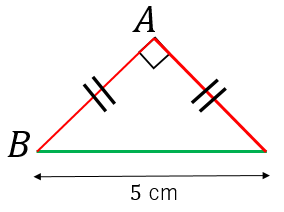
つまり、内角がそれぞれ90°、45°、45°の二等辺三角形の三辺の比は、1:1:√2となるのです。 公式 直角二等辺三角形の辺の長さの比:1:1:√2 この公式はかなりの頻度で利用する必要が生まれますので、是非とも覚えてしまうことをおすすめします。




二等辺三角形 Wikipedia



二 等辺 三角形 辺 の 長 さ 直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 Stg Origin Aegpresents Com



二 等辺 三角形 辺 の 長 さ 直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 Stg Origin Aegpresents Com




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



二等辺三角形とは 定義 定理や 角度 辺 面積の求め方 受験辞典



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



Download 二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め Images For Free




Oahjarnmevzlmm



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学
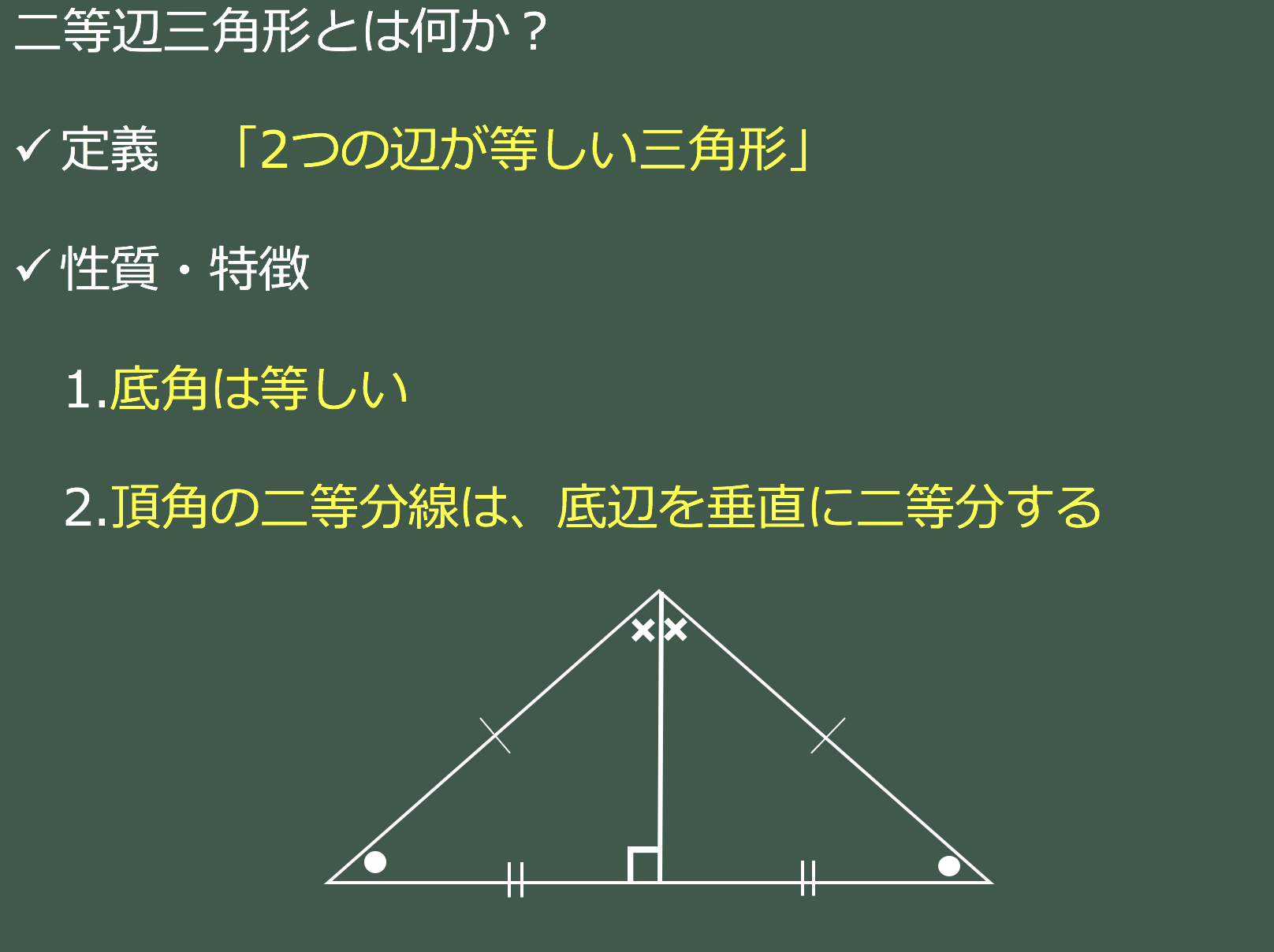



3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ
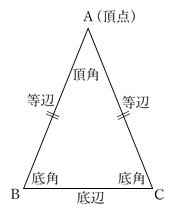



三角形 四角形 おやじさん ネット




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




頂角が45 の二等辺三角形の面積 中学数学 Youtube
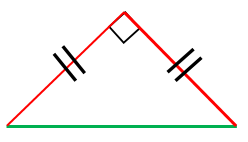



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



至急お願いします 中3の数学の問題で斜辺が1cm 底角が75 Yahoo 知恵袋
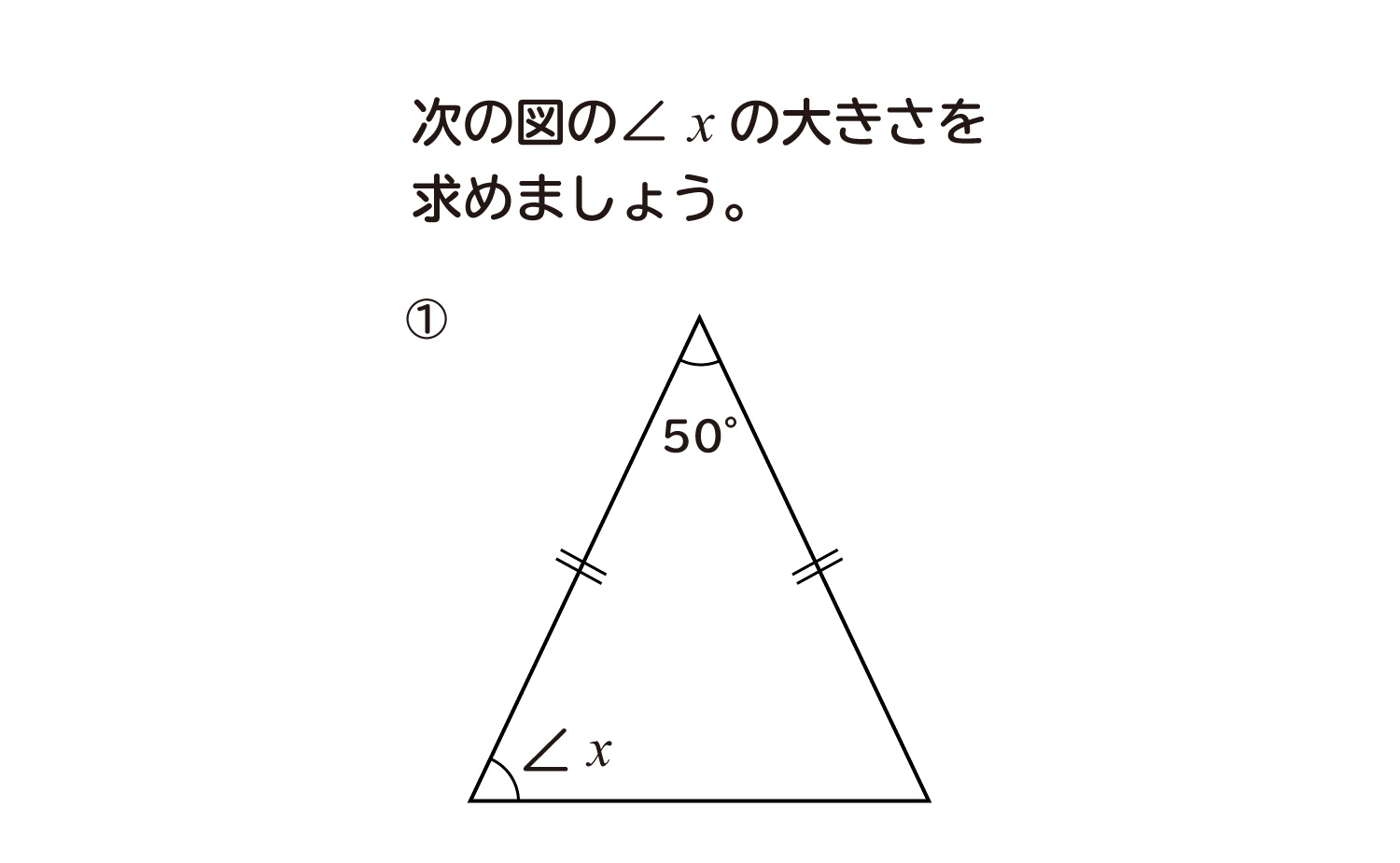



中学2年生 数学 無料問題集 二等辺三角形の角を求める おかわりドリル




各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア
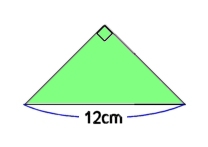



直角二等辺三角形
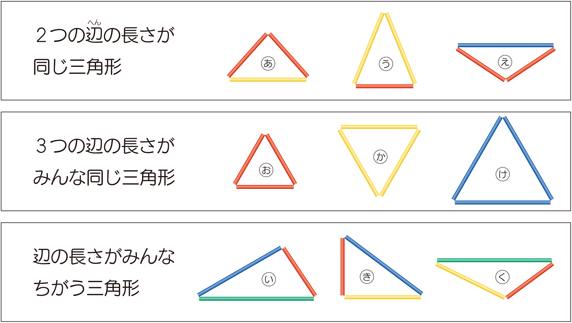



二等辺三角形と正三角形 算数用語集




二 等辺 三角形 辺 の 長 さ 直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 Stg Origin Aegpresents Com



3
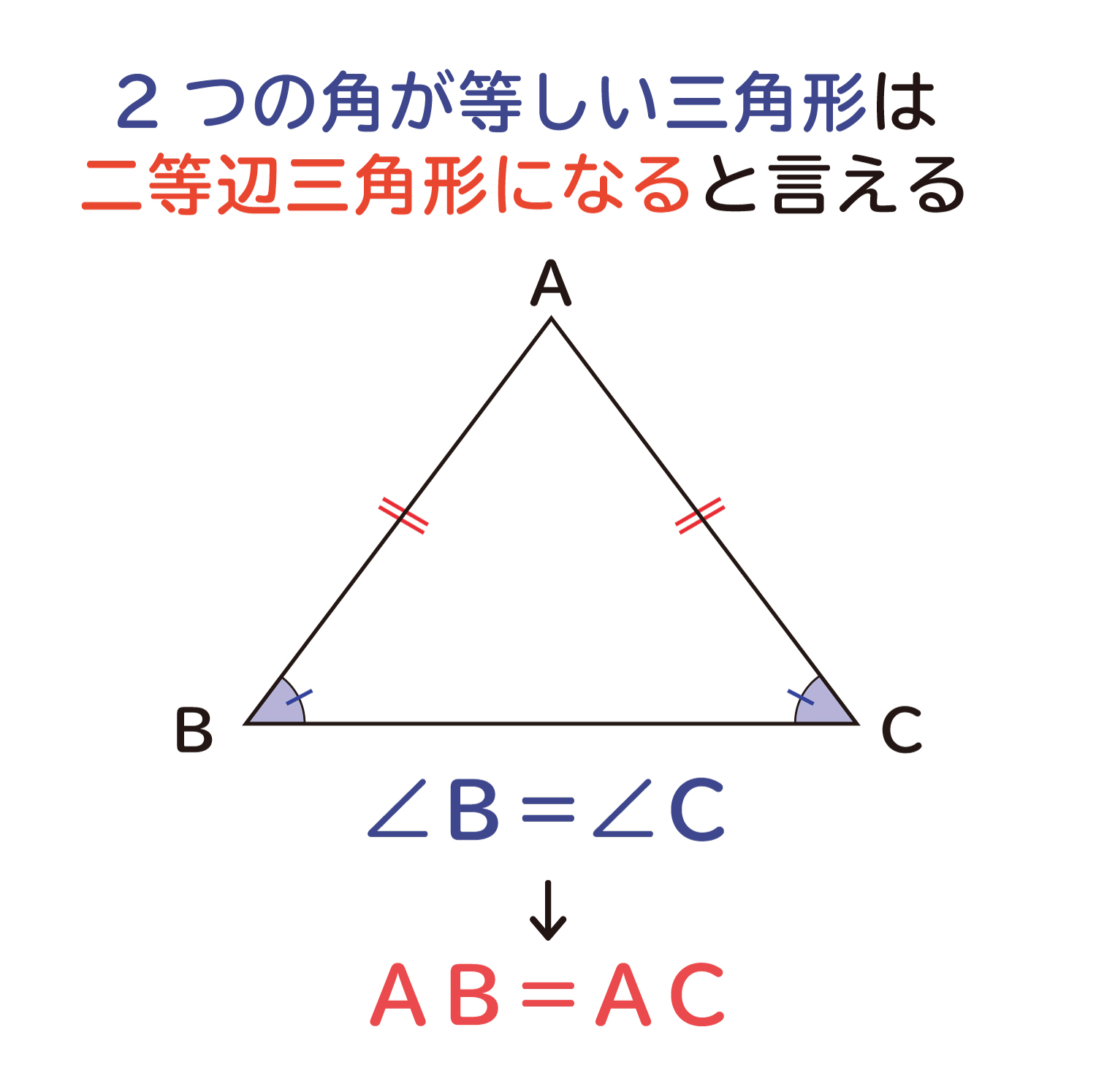



2つの角が等しい三角形は 二等辺三角形になる ことの説明 おかわりドリル
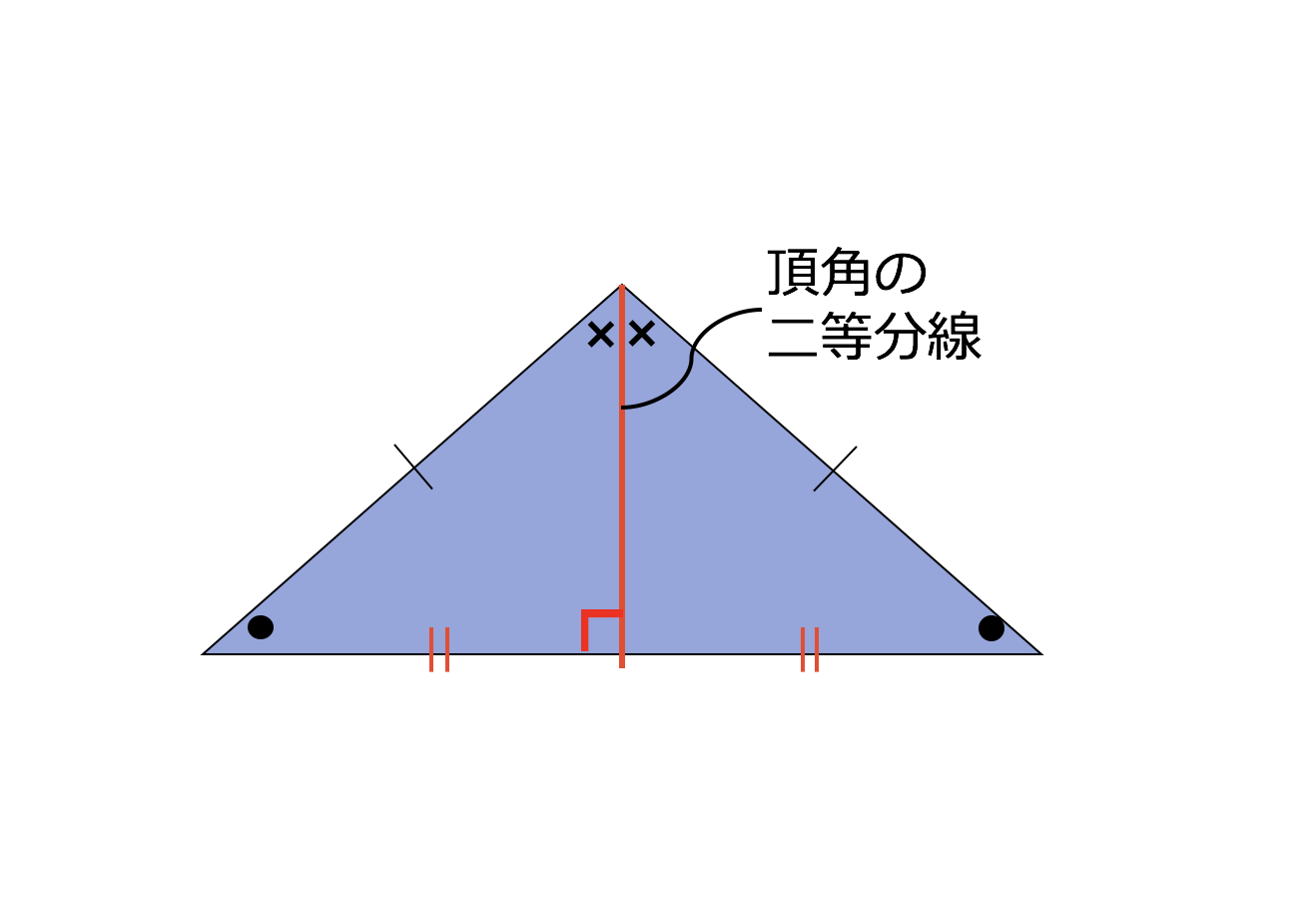



3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




二等辺三角形の定義と定理 算数 数学が好きになりmath




二等辺三角形の底辺の長さを弦 辺a 辺bの長さを弧とした場合の高さの 数学 教えて Goo




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
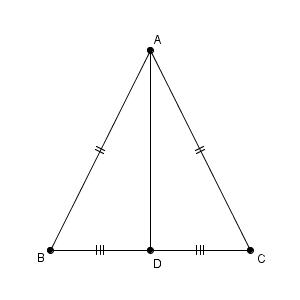



標準 ベクトルの内積と二等辺三角形 なかけんの数学ノート
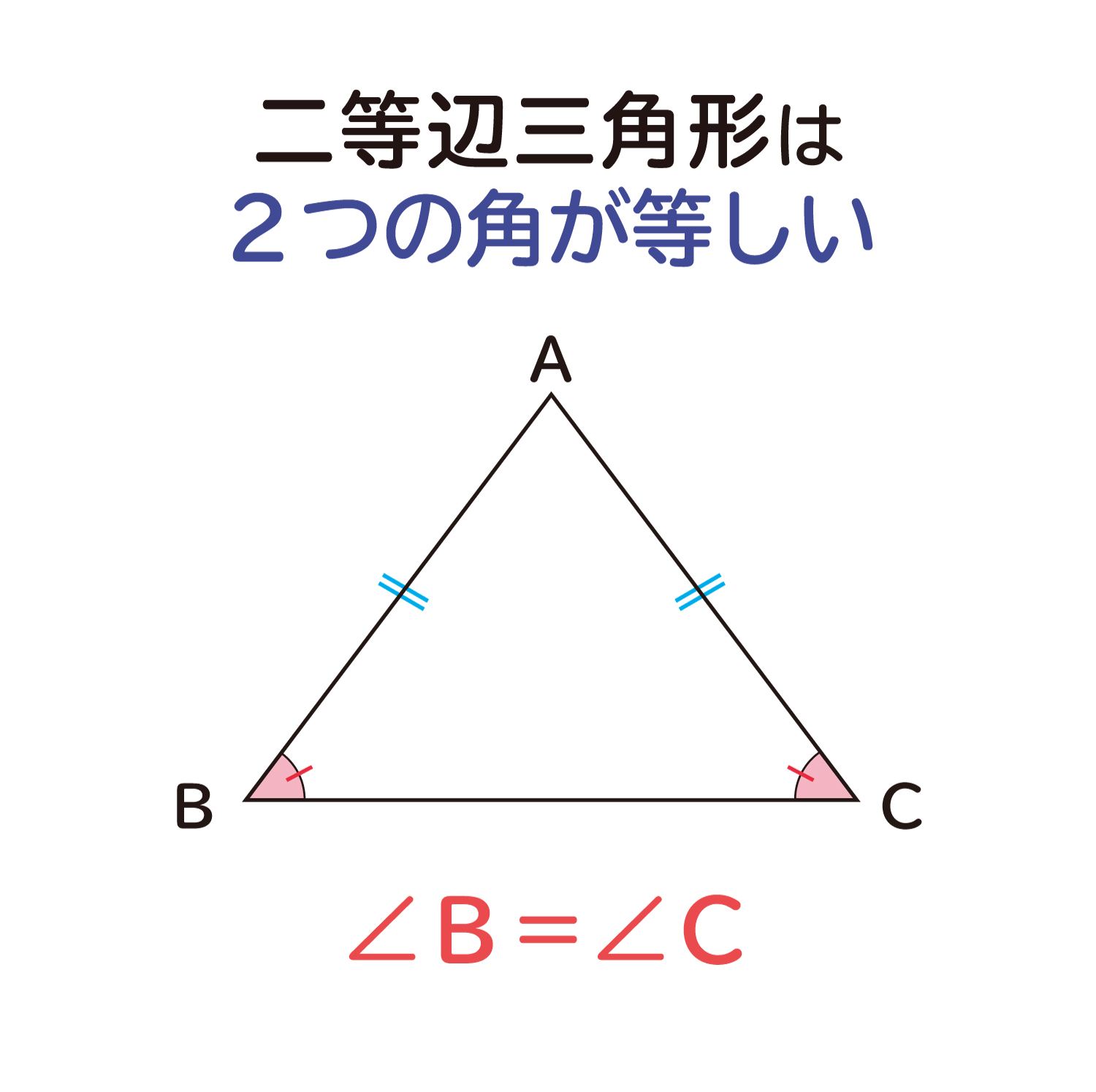



二等辺三角形の2つの角は等しくなる ことの説明 おかわりドリル



3年算数 三角形と角 の教え方



二等辺三角形abcの底辺bcの中点mから それぞれ辺ab Acに垂 Yahoo 知恵袋
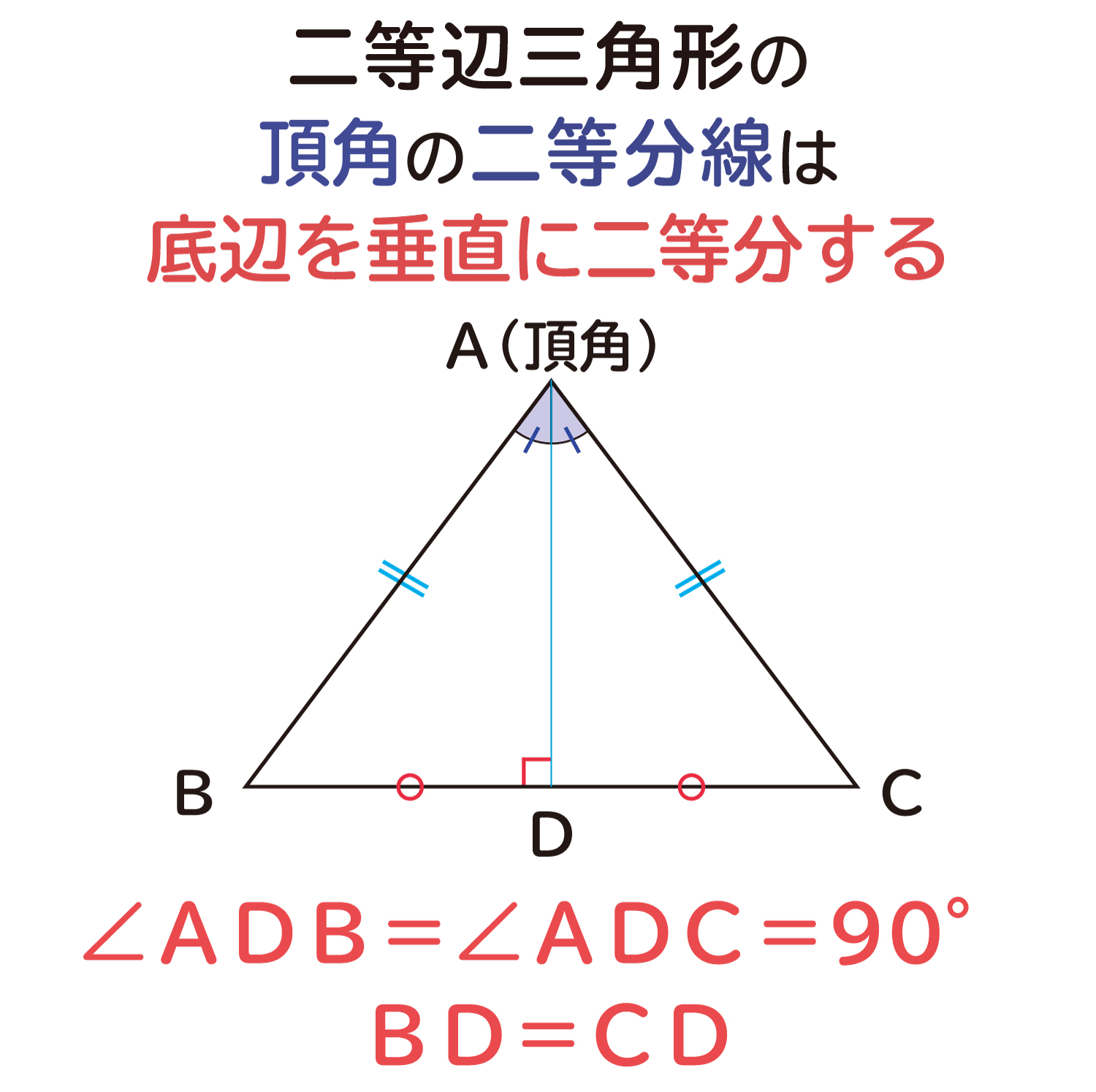



二等辺三角形の頂角の二等分線は 底辺を垂直に二等分する ことの説明 おかわりドリル




二等辺三角形の頂角の二等分線は底辺を垂直に二等分する Youtube




二等辺三角形の性質 Youtube



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




直角二等辺三角形の中のとある点を求めたい こんばんわ 直角二等辺三角形a Okwave




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
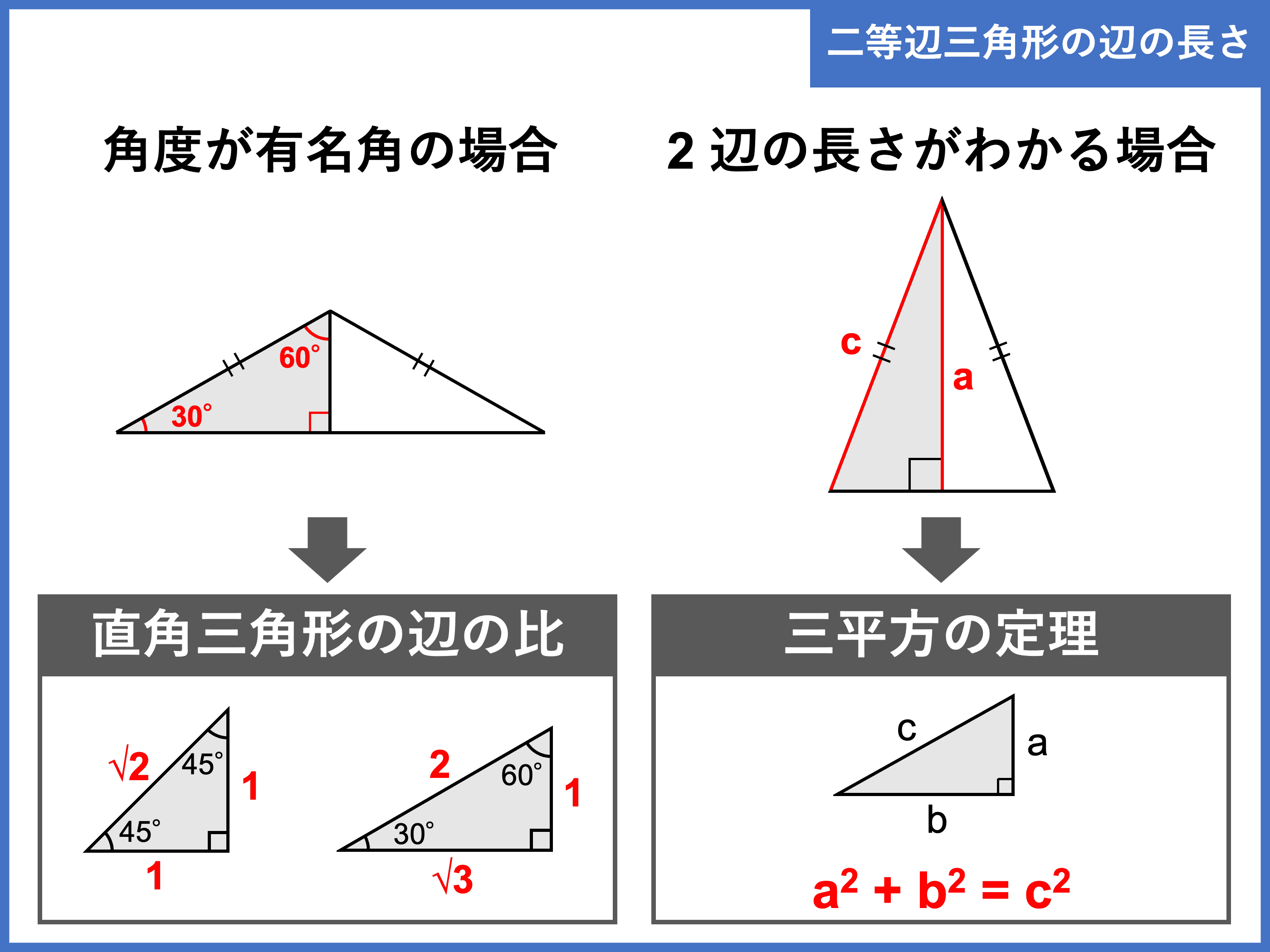



二等辺三角形とは 定義 定理や 角度 辺 面積の求め方 受験辞典




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者



3
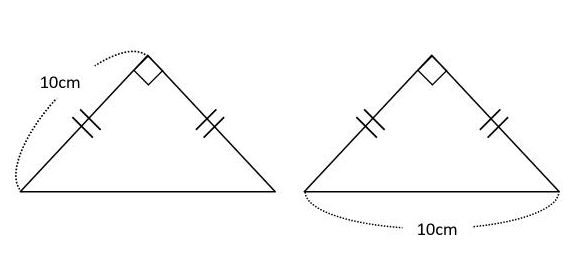



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




二等辺三角形の定義と性質 問題の解き方 数学fun



二等辺三角形とは 定義 定理や 角度 辺 面積の求め方 受験辞典
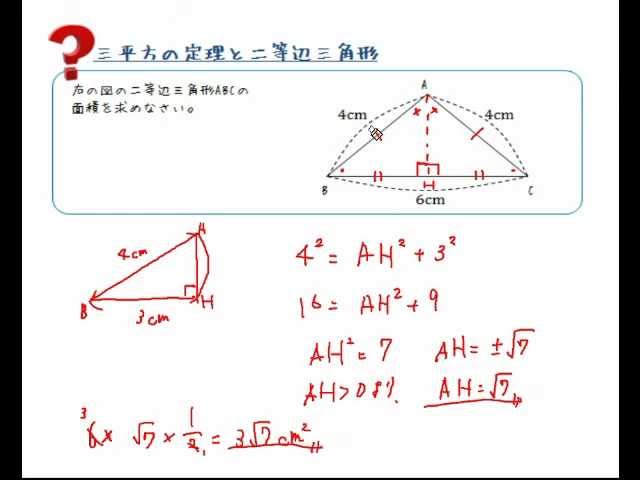



三平方の定理と二等辺三角形 Youtube



二等辺三角形の公式 面積 高さ 角度 斜辺と周囲の長さ 数学 エクセルマニア
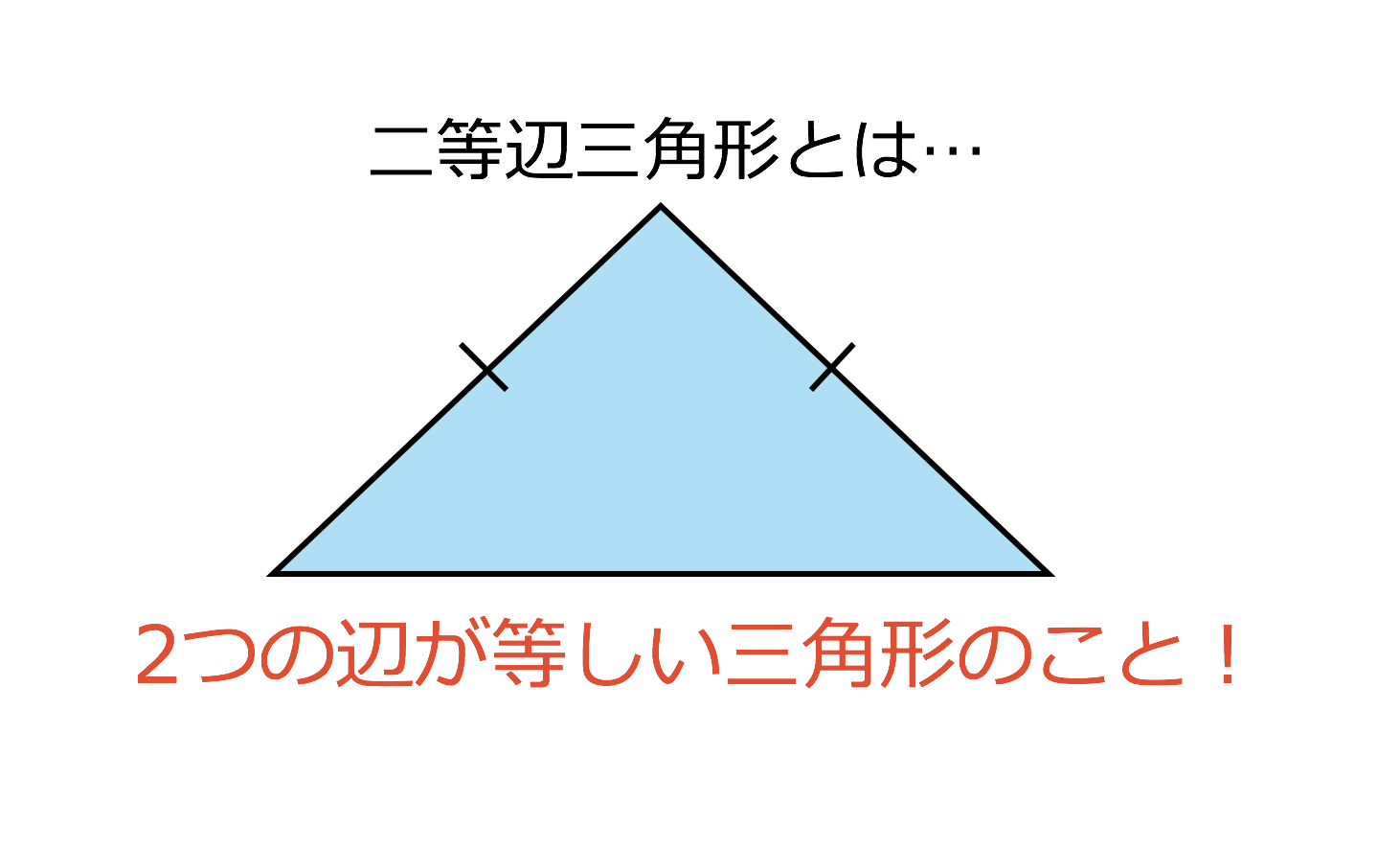



3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ
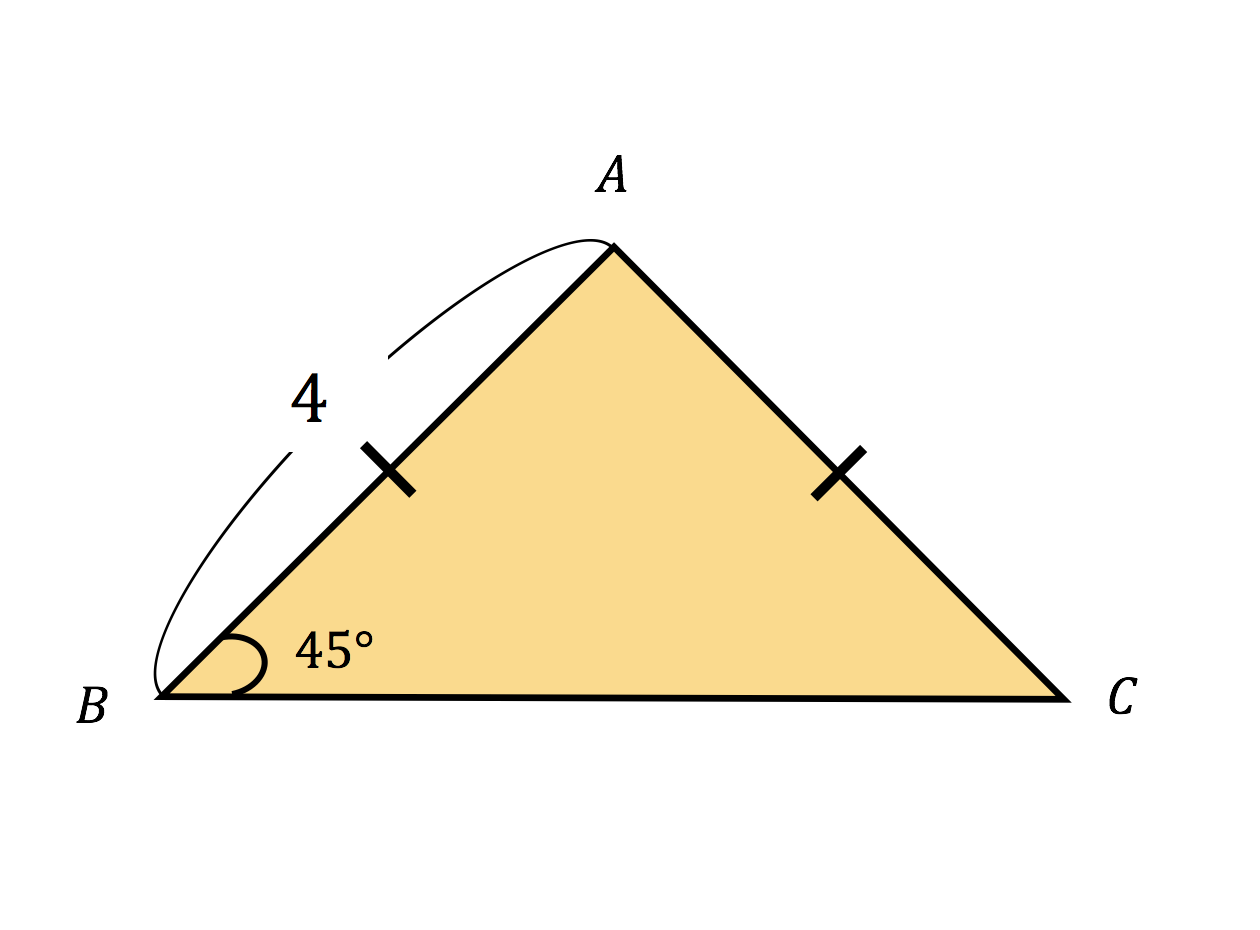



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



3




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう



3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ



今 二等辺三角形が熱い 小学校の算数が懐かしい デイリーポータルz



1
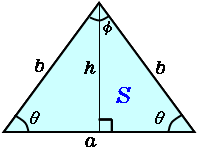



二等辺三角形 高精度計算サイト




中2数学 二等辺三角形の性質2 頂角の二等分線 練習編 映像授業のtry It トライイット
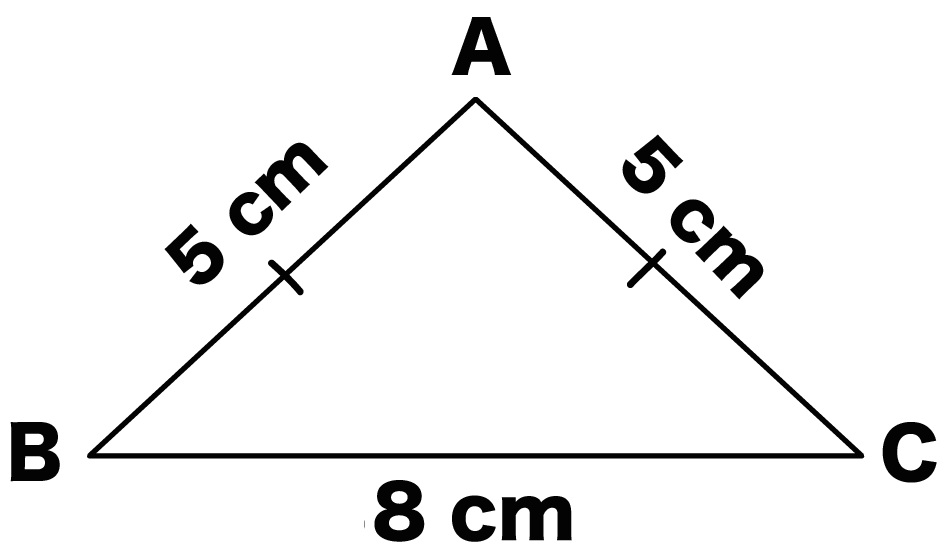



簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
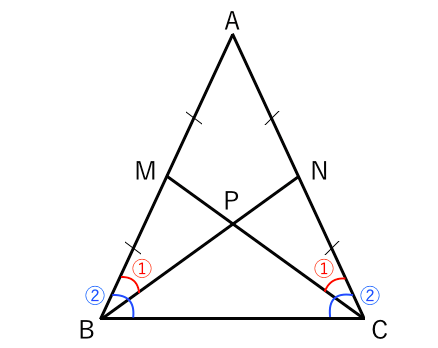



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に



二等辺三角形とは 定義 定理や 角度 辺 面積の求め方 受験辞典



二等辺三角形の底辺を三等分し その各等分した点から頂点に線を Yahoo 知恵袋




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



絶対に覚えるべきもうひとつの三角形 父ちゃんが教えたるっ
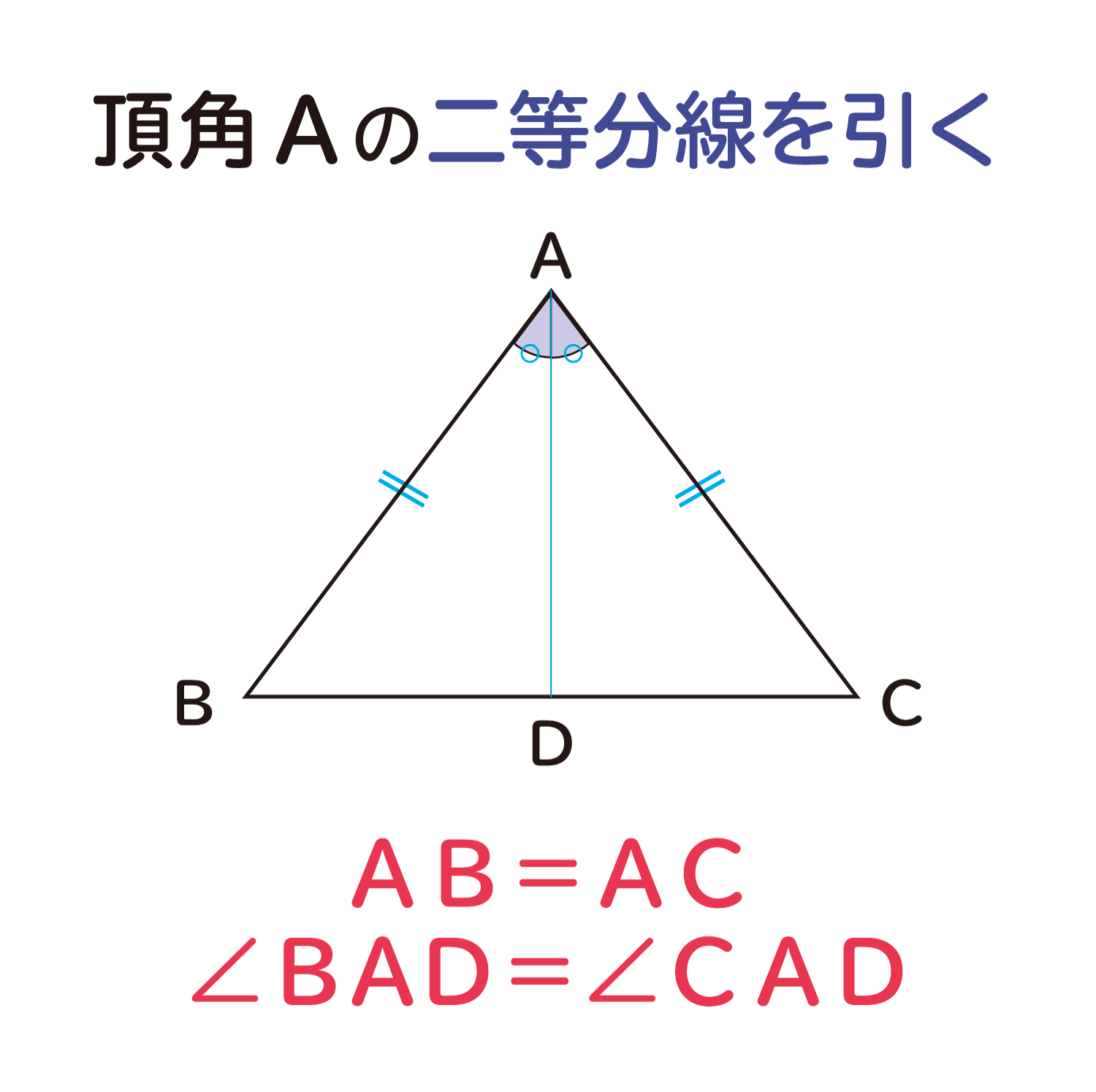



二等辺三角形の頂角の二等分線は 底辺を垂直に二等分する ことの説明 おかわりドリル
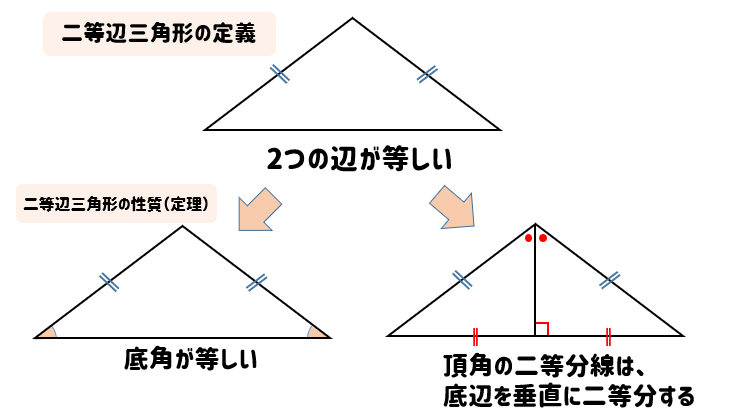



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ
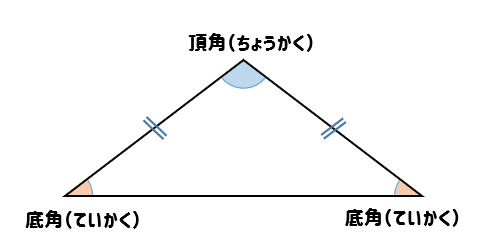



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ
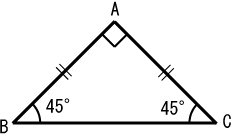



直角二等辺三角形 Wikipedia
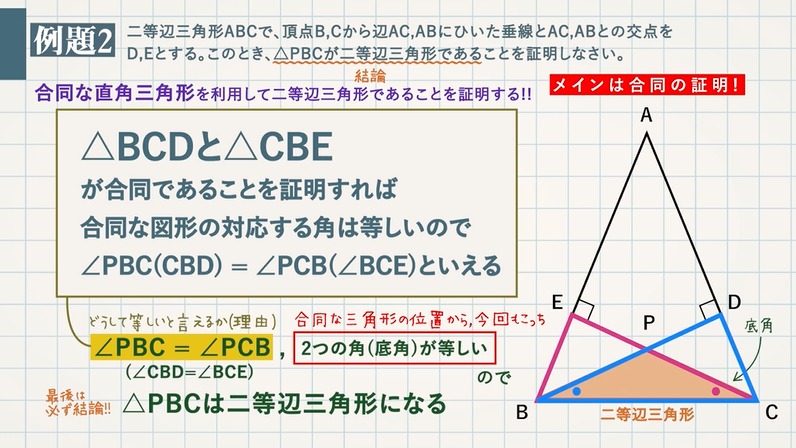



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋
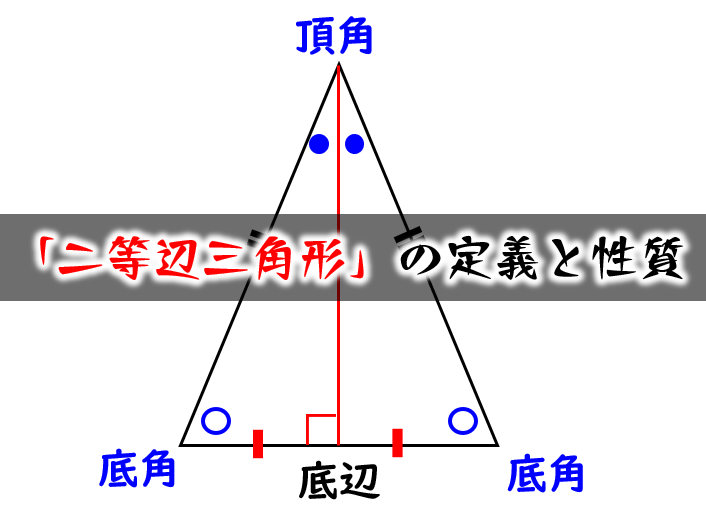



二等辺三角形の定義と性質 問題の解き方 数学fun




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
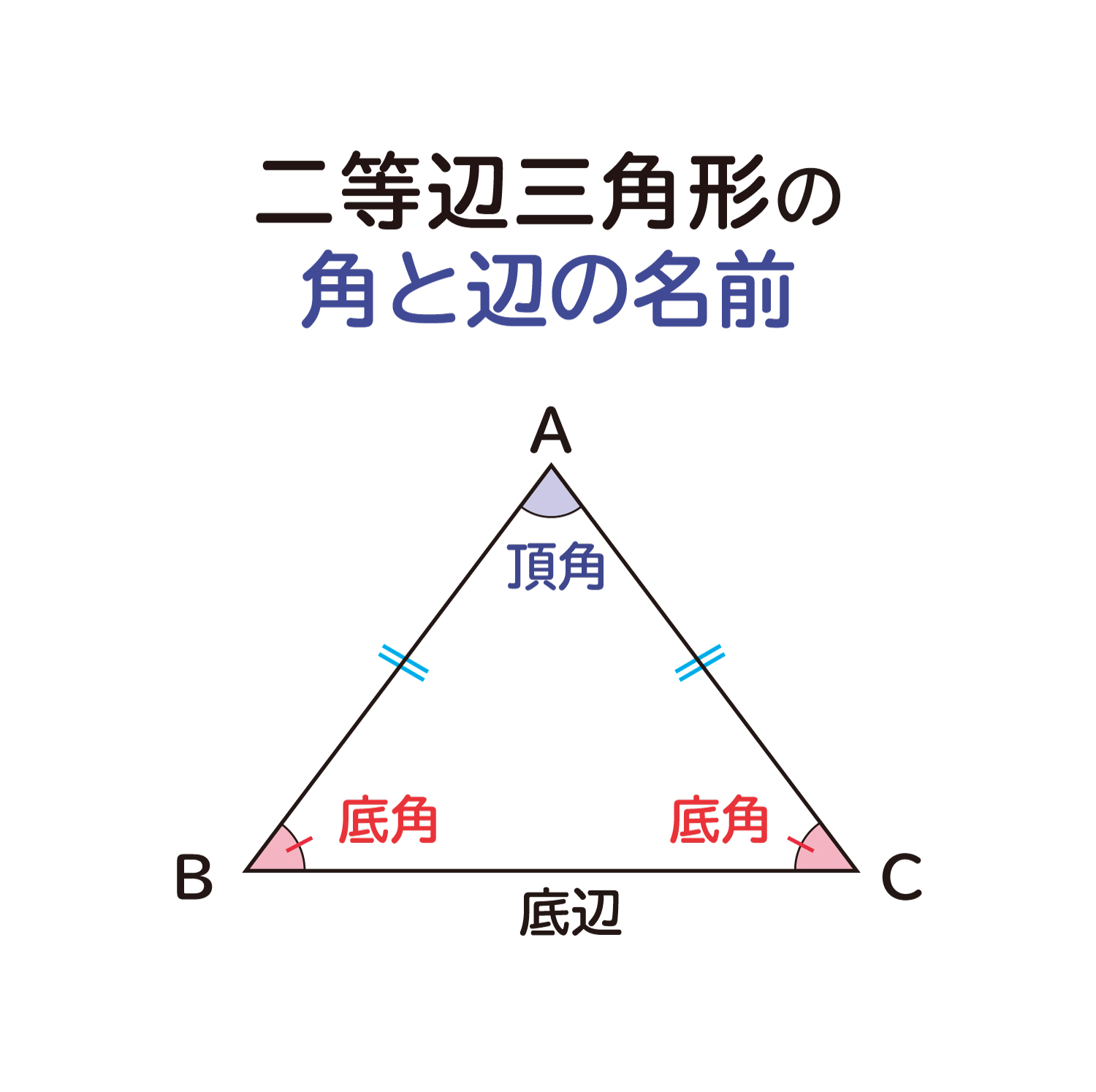



二等辺三角形の頂角の二等分線は 底辺を垂直に二等分する ことの説明 おかわりドリル
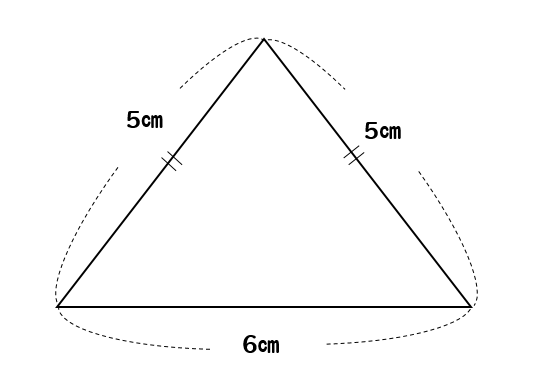



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
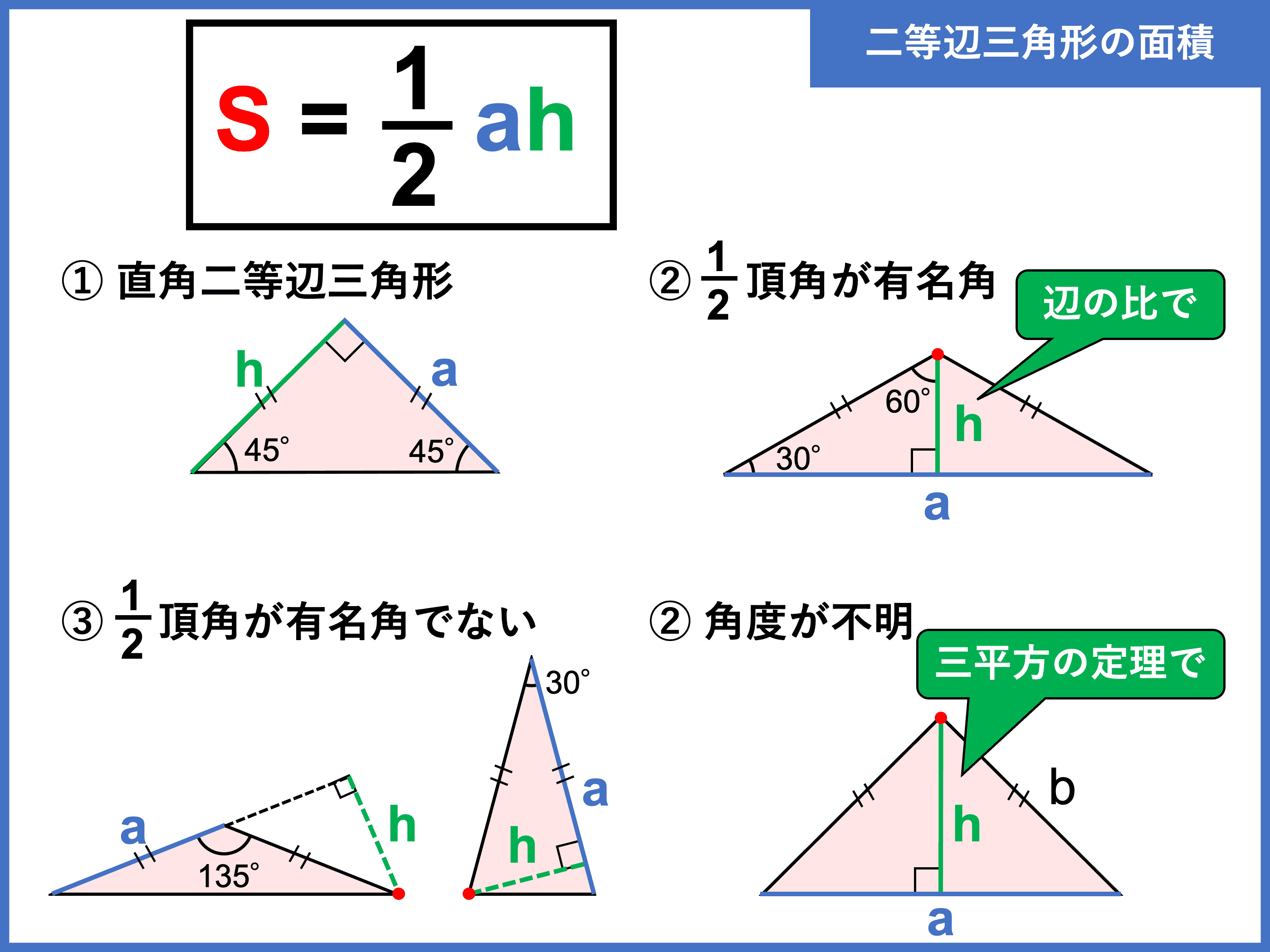



二等辺三角形とは 定義 定理や 角度 辺 面積の求め方 受験辞典
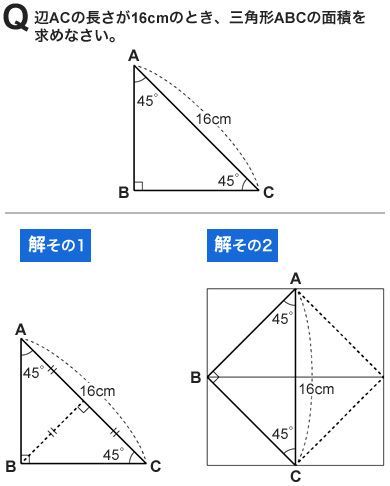



256が解ける子解けない子の差 4つの解法をすぐ思いつくか 2ページ目 President Online プレジデントオンライン




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
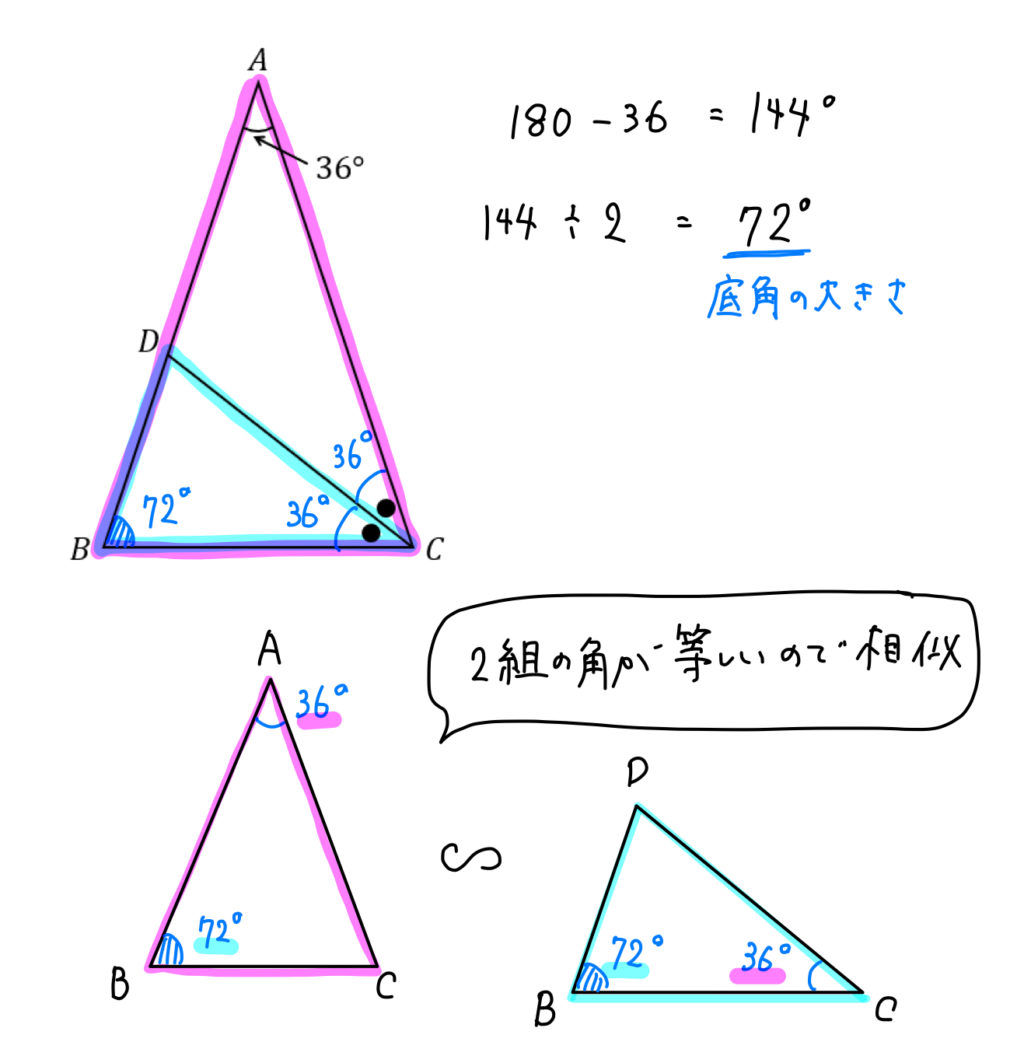



数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明
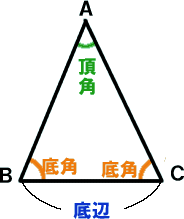



二等辺三角形




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ
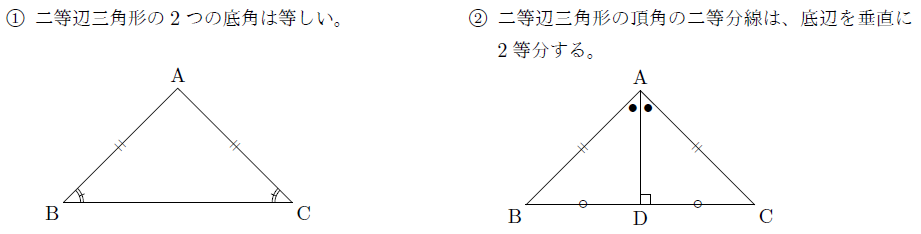



二等辺三角形の性質 まなびの学園



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



二等辺三角形の面積教えてください 斜辺が2cm頂角30度底辺の角 Yahoo 知恵袋




二等辺三角形に関するある問題 底辺 高さそして面積 身勝手な主張




二等辺三角形になることの証明 Youtube



0 件のコメント:
コメントを投稿